세그먼트 트리

세그먼트 트리의 설명과 구현

컴퓨터 과학에서, 세그먼트 트리(통계학적 트리로도 부름)는 간격이나 부분에 대한 정보를 저장하는데 사용되는 트리 데이터 구조입니다. 저장된 부분 중 어느 것이 주어진 포인트를 포함하는지 쿼리할 수 있습니다. 세그먼트 트리는 원칙적으로 정적 구조여서 일단 생성되면 구조를 변경할 수 없습니다. 비슷한 데이터 구조로는 간격 트리가 있습니다.

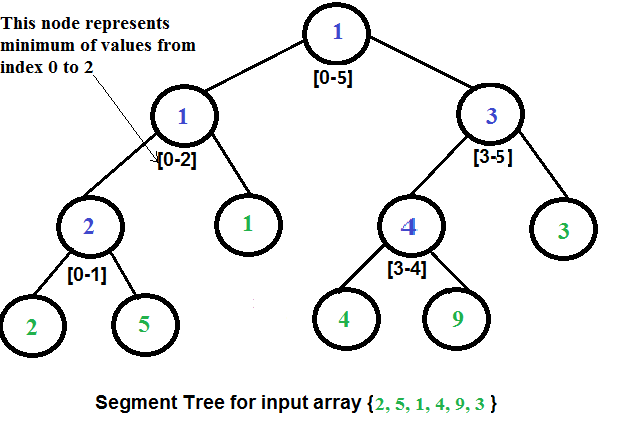
세그먼트 트리는 이진 트리입니다. 트리의 루트는 전체 배열을 나타냅니다. 루트의 두 자식은 배열의 첫 번째 절반과 두 번째 절반을 나타냅니다. 유사하게, 각 노드의 자식은 노드에 해당하는 배열의 두 절반에 해당합니다.

트리는 상향식으로 만드는데, 각 노드의 값이 자식 노드 중 가장 “최소”(또는 다른 함수)인 값이어야 합니다. 이것은 O(n log n)의 시간이 걸립니다. 수행한 작업 수는 트리 높이(O(log n))입니다.

범위 쿼리를 수행하기 위해 각 노드는 각 자식 노드에 하위 쿼리 하나씩, 쿼리를 두 부분으로 나눕니다. 쿼리에 노드의 부분배열 전체가 포함된 경우 노드에서 미리 계산된 값을 사용할 수 있습니다. 이 최적화를 사용하면 O (log n)의 최소 작업만 수행되었음을 증명할 수 있습니다.

응용

세그먼트 트리는 특정 배열 작업, 특히 범위 쿼리와 관련된 작업을 효율적으로 수행하도록 설계된 데이터 구조입니다.

세그먼트 트리의 응용은 전산 기하학과 지리 정보 시스템 분야에 있습니다.

세그먼트 트리의 현재 구현은 바이너리 (2개의 입력 매개 변수 포함) 함수를 전달할 수 있으므로 다양한 함수에 대한 범위 쿼리를 수행 할 수 있음을 의미합니다.

테스트에서 SegmentTree에서 min, max 및 sum 범위 쿼리를 수행하는 예를 찾을 수 있습니다.

요약

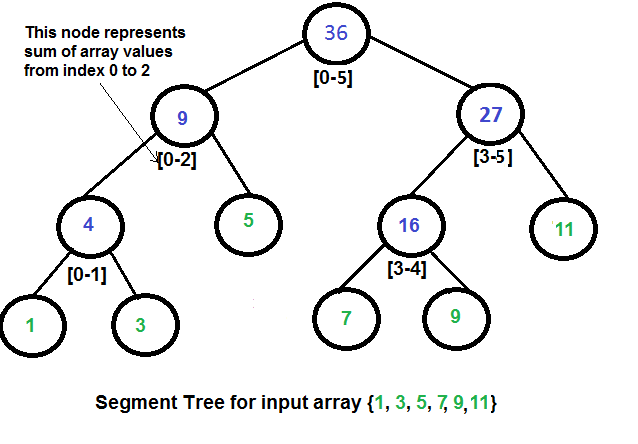
배열에서 특정 범위의 정보(최소, 최대, 합계)를 빠르게(O(log n)) 얻을 수 있다.

ex)

• 인덱스 2에서 10 사이의 최소값
• 인덱스 5에서 20 사이의 합

구현

export default class SegmentTree {
  /**
   * @param {number[]} inputArray
   * @param {function} operation - sum, min 같은 이항 함수
   * @param {number} operationFallback - sum의 0이나 min의 Infinity 같은 연산의 fallback 값
   */
  constructor(inputArray, operation, operationFallback) {
    this.inputArray = inputArray;
    this.operation = operation;
    this.operationFallback = operationFallback;

    // 세그먼트 트리를 표현하는 배열 생성 (실제 트리 구조를 사용하지 않는다.)
    this.segmentTree = this.initSegmentTree(this.inputArray);

    this.buildSegmentTree();
  }

  initSegmentTree(inputArray) {
    let segmentTreeArrayLength;
    const inputArrayLength = inputArray.length;

    if (isPowerOfTwo(inputArrayLength)) {
      // 원본 배열의 길이가 2의 배수라면
      segmentTreeArrayLength = 2 * inputArrayLength - 1;
    } else {
      // 원본 배열의 길이가 2의 배수가 아니라면
      // 배열 길이보다 큰 2의 배수 가장 작은 값을 찾는다.
      // 완전 이진 트리를 만들어서 빈 공간을 null로 채워야하기 때문이다.
      const currentPower = Math.floor(Math.log2(inputArrayLength));
      const nextPower = currentPower + 1;
      const nextPowerOfTwoNumber = 2 ** nextPower;
      segmentTreeArrayLength = 2 * nextPowerOfTwoNumber - 1;
    }

    return new Array(segmentTreeArrayLength).fill(null);
  }

  // 세그먼트 트리 만들기
  buildSegmentTree() {
    const leftIndex = 0;
    const rightIndex = this.inputArray.length - 1;
    const position = 0;
    this.buildTreeRecursively(leftIndex, rightIndex, position);
  }

  // 세그먼트 트리를 재귀적을 만든다.
  buildTreeRecursively(leftInputIndex, rightInputIndex, position) {
    // 작은 인덱스랑 큰 인덱스가 같다면 배열 나누는 게 끝났으니 Leaf 노드에 도착했다는 뜻이다.
    // 입력 배열에서 세그먼트 트리로 Leaf 값을 복사한다.
    if (leftInputIndex === rightInputIndex) {
      this.segmentTree[position] = this.inputArray[leftInputIndex];
      return;
    }

    // 배열을 둘로 나눠서 각각 재귀적으로 처리한다.
    // (0 ~ 9)면 (0 ~ 4), (5 ~ 9) 둘로 나뉨
    const middleIndex = Math.floor((leftInputIndex + rightInputIndex) / 2);
    // 왼쪽
    this.buildTreeRecursively(
      leftInputIndex,
      middleIndex,
      this.getLeftChildIndex(position)
    );
    // 오른쪽
    this.buildTreeRecursively(
      middleIndex + 1,
      rightInputIndex,
      this.getRightChildIndex(position)
    );

    // 모든 Leaf 노드가 다 찼으니(위의 if문에서 채움)
    // 주어진 연산 함수를 써서 트리를 상향식으로 채운다.
    this.segmentTree[position] = this.operation(
      this.segmentTree[this.getLeftChildIndex(position)],
      this.segmentTree[this.getRightChildIndex(position)]
    );
  }

  // this.operation function에 맞게 범위 쿼리를 실행한다.
  rangeQuery(queryLeftIndex, queryRightIndex) {
    const leftIndex = 0;
    const rightIndex = this.inputArray.length - 1;
    const position = 0;

    return this.rangeQueryRecursive(
      queryLeftIndex,
      queryRightIndex,
      leftIndex,
      rightIndex,
      position
    );
  }

  // 범위 쿼리를 재귀적으로 실행
  rangeQueryRecursive(
    queryLeftIndex,
    queryRightIndex,
    leftIndex,
    rightIndex,
    position
  ) {
    if (queryLeftIndex <= leftIndex && queryRightIndex >= rightIndex) {
      // 범위가 완전히 겹칠 때
      return this.segmentTree[position];
    }

    if (queryLeftIndex > rightIndex || queryRightIndex < leftIndex) {
      // 안 겹침
      return this.operationFallback;
    }

    // 부분적으로 겹칩
    const middleIndex = Math.floor((leftIndex + rightIndex) / 2);

    const leftOperationResult = this.rangeQueryRecursive(
      queryLeftIndex,
      queryRightIndex,
      leftIndex,
      middleIndex,
      this.getLeftChildIndex(position)
    );

    const rightOperationResult = this.rangeQueryRecursive(
      queryLeftIndex,
      queryRightIndex,
      middleIndex + 1,
      rightIndex,
      this.getRightChildIndex(position)
    );

    return this.operation(leftOperationResult, rightOperationResult);
  }

  // 왼쪽 자식 인덱스
  getLeftChildIndex(parentIndex) {
    return 2 * parentIndex + 1;
  }

  // 오른쪽 자식 인덱스
  getRightChildIndex(parentIndex) {
    return 2 * parentIndex + 2;
  }
}

참고

 

• Wikipedia
• YouTube
• GeeksForGeeks

출처

• Github